Recuerdo, como siempre se suele hacer, aunque me parece que todo el mundo se acuerda, que un número primo es todo aquel número que sólo puede dividirse por 1 y por él mismo.
En principio, uno puede preguntarse qué... demonios tiene eso de importante para estar dándole tantas vueltas al tema. Como respuesta a esta pregunta, recomiendo que se vuelva a la entrada "¿Para qué conocer los números primos?". Ahí encontrarás, además de razones puramente matemáticas, otra razón puramente económica. Eso sí, la recompensa económica tiene que ser para los que no estén realmente desesperados (o sí...) porque para el problemita de encontrar la expresión general de los números primos parece que hay que armarse de paciencia y de fuerza.
 | |||
| Christian Goldbach |
“Todo número par mayor que 2 puede escribirse como suma de dos números primos”
Lo que está claro es que si no contamos el 2, todos los primos son impares y, por tanto, al sumar dos de ellos, el resultado va a ser par. También es verdad que cualquier número par lo podemos escribir como suma de dos números impares... Pero eso no significa que se puedan escribir como suma de dos primos.
¿Por qué se llama a tal cosa “conjetura”? Porque aún no se ha demostrado... Y hasta que no se demuestre, no dejará de ser algo que parece que se cumple, pero que no se tiene la seguridad de que funcione en todos los casos, ni de por qué funciona.
Un mes después de recibir la carta, Euler contestó a Goldbach que había comprobado que la conjetura era cierta hasta el número 1000:
4 =2 + 2 ; 6 = 3 + 3 ; 8 = 3 + 5 ; 10 = 3 + 7 ; 12 = 5 + 7 ...
Y así hasta hacerlo con el 1000. No satisfecho, tres meses y medio más tarde volvió a contestarle que lo había probado con éxito hasta el número 2500. Pero este método para comprobar que lo que Goldbach dijo era cierto era totalmente inviable... Para empezar, hay infinitos números pares... Sólo con esto, sería suficiente para comprender que llevaría, literalmente, una eternidad comprobarlo número por número. Aún así, también hay que añadir, que no conocemos todos los números primos... Así que, si para números muy grandes, necesitamos números primos muy grandes... Una razón de más para buscar otra estrategia.
¿Qué otra estrategia seguir para demostrar la conjetura de Goldbach? Eso quisieran saber muchos. No deja de chocar el hecho de que un enunciado tan sencillo, que todo el mundo “no matemático” puede comprender, sea uno de los problemas más importantes y difíciles de las Matemáticas hoy en día.
Mientras algunos le dan vueltas a la cabeza, hoy en día se le encargan a los ordenadores que hagan la tediosa tarea de seguir comprobando la conjetura... El récord parece ser que está en el número 1.000.000.000.000.000.000.
Marcus du Sautoy dice que los números primos son como los átomos que componen a las moléculas que serían el resto de los números. Esta comparación de átomos y números primos se basa en la "descomposición en factores primos" que se enseña en 1º ESO. Por ejemplo:
Marcus du Sautoy dice que los números primos son como los átomos que componen a las moléculas que serían el resto de los números. Esta comparación de átomos y números primos se basa en la "descomposición en factores primos" que se enseña en 1º ESO. Por ejemplo:
Con la conjetura de Goldbach, los números pares volverían a ser "moléculas" diatómicas... Eso sí, el "enlace" entre los "átomos-primos" sería en este caso la operación suma y esta "descomposición" no siempre es única:
24 = 11+13
90 = 7+ 83 = 43 + 47
Como curiosidad, la conjetura de Goldbach es mencionada en la película: "La verdad oculta" (2005), que trata de una joven matemática, hija también de un matemático. El padre (Anthony Hopkins) muere y a la hija (Gwyneth Paltrow) le preocupa haber heredado, no sólo su gusto y habilidad para las Matemáticas, sino su enfermedad mental. La conjetura de Goldbach también aparece en la película española "La habitación de Fermat" (2007).
Bibliografía:
- “Los números primos. Un largo camino al infinito”. Enrique Cracián. Ediciones RBA.
- http://es.wikipedia.org/wiki/Conjetura_de_Goldbach
- http://buscabiografias.com/bios/biografia/verDetalle/8558/Christian%20Goldbach
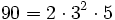
No hay comentarios:
Publicar un comentario