Fronteras, costas... Los bordes no son "perfectos"

Desde el comienzo de la Geometría nos hemos acostumbrado a ver o a resaltar las formas más simples en la naturaleza: se pensó que la Luna y los demás astros eran esferas (después tenía un cierto achatamiento), vemos líneas rectas, parábolas, rectas paralelas, triángulos, paralelogramos... Y a lo largo de la historia hemos utilizado esas formas para conocer y describir cuanto nos rodea. Pero la observación con más detalle nos da otra imagen, nos vemos obligados a crear otras herramientas y las Matemáticas se enriquecen.
(Clicar sobre las imágenes para verlas más grandes)

En el siglo XX Lewis Fry Richardson (1881-1953) investigó acerca de la relación entre la longitud de la frontera entre países y la propensión a la guerra de estos (curioso, pero lo investigó). Para ello recopiló datos de la longitud de fronteras y cuál sería su sorpresa cuando descubrió que no existía un acuerdo sobre estas medidas. Por ejemplo, según España, la longitud de la frontera con Portugal era de 987 Km, mientras que Portugal medía para la misma longitud 1214 Km. Lo mismo ocurría en el resto de Europa. ¿Cómo era esto posible? La respuesta a esta pregunta no radica en intereses particulares de cada país, sino en algo más elemental: la unidad de medida que se utilizaba, como se va a comentar a continuación.

Frontera con de Portugal-Cáceres

Efectivamente, las líneas que definen la frontera entre dos países o la de tierra-mar en el caso de las costas son líneas muy "rugosas", muy irregulares,  con innumerables entrantes y salientes de diferente tamaño, muy diferentes de las líneas que forman las figuras geométricas que vienen en los libros de texto. Imaginemos ahora que medimos la frontera anterior (España-Portugal) desde el espacio exterior, desde donde apenas distinguiríamos las irregularidades. La longitud que obtendríamos sería mucho menor que el que obtendríamos desde tierra utilizando como instrumento un enorme compás imaginario abierto 100 Km. Supongamos que después volvemos a medir, pero el compás lo abrimos 10 Km. Puesto que ahora el compás está diez veces menos abierto, habremos medido muchos más entrantes y salientes de la línea de frontera y la longitud obtenida tendrá mayor precisión y será mayor. Si la medida la realizamos con el compás abierto 1 Km, habremos medido aún más entrantes y salientes de la frontera y la longitud será más precisa y aún mayor a la obtenida anteriormente. Así podríamos seguir sucesivamente... Y uno se puede preguntar: ¿qué valor obtendríamos si tuviésemos el tamaño de una hormiga y el compás fuese diminuto?. En este caso, la cantidad de entrantes y salientes que iríamos encontrando durante la medida sería muchísimo mayor... Y la longitud de la frontera que obtendríamos sería mucho mayor también.
En resumen, la longitud de la frontera aumenta conforme disminuye la unidad de medida utilizada (o aumenta la precisión del instrumento de medida). Este es el llamado efecto Richardson.
Llegados a este punto, la noción de longitud que se tenía hasta ahora no resulta adecuada para este tipo de líneas tan irregulares. Se tiene que idear otra idea, otro número que cuantifique cómo estas líneas llenan el espacio. Este número viene dado por el exponente "d" de la siguiente expresión:

Donde L es la longitud de la frontera, c es una constante que depende la frontera que se mida y s es la unidad de medida.
Es obvio en la expresión anterior que la longitud L depende de la unidad de medida, de la escala en la que se mide la frontera. Cuánto menor sea "s" (mayor escala), mayor será L. Por otro lado, se puede decir que 1/s indica la precisión (cuanto menor es "s" mayor es la precisión 1/s), así que cuanto mayor sea la precisión, mayor será la longitud medida L.
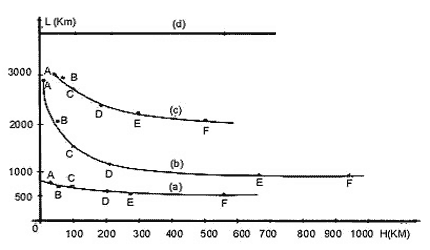
Cuanto mayor sea el número "d" mayor es la rugosidad o irregularidad de la línea de frontera. En la gráfica siguiente se representan los valores de L para distintas "s" (H en la gráfica) en el caso de algunas fronteras:

La gráfica a) corresponde a la frontera España-Portugal, a la que le corresponde una d=0,14. La curva b) corresponde a la frontera terrestre de Alemania (1900) con d=0,15 y la curva c) a la costa occidental de Gran Bretaña, una de las más recortadas del planeta y que tiene una d=0,25.

Gran Bretaña, una de
las costas más irregulares

Sudáfrica, una de las costas
más uniformes

Otros datos son d=0,02 para la costa de Sudáfrica, una de las más uniformes del planeta y d=0,13 para la costa de Australia (parecida a la de España y Portugal).

En la imagen anterior aparece también la gráfica que obtendríamos si midiésemos la longitud de una circunferencia a distintas escalas e). En este caso, al igual que con cualquier polígono regular, el perímetro que mediríamos no depende de la escala o unidad de medida. Si imaginamos una circunferencia de 100 Km de diámetro, el perímetro viene dado por la expresión ya archiconocida:

Si en lugar de calcular el diámetro, lo midiésemos con un compás abierto 50 Km (lo que equivale a aproximar la circunferencia a un hexágono regular), la longitud obtenida sería de 300 Km. Para una unidad de medida inferior, aproximando la circunferencia a un polígono regular de 12 lados, la aproximación seria de 310, 584 Km. Para una aproximación de un polígono de 24 lados, el perímetro medido sería de 313,272 Km... Aproximando a un polígono de 192 lados se obtendría una medida de 314,112 Km. En resumen en las figuras geométricas que aprendemos en los institutos la medida del perímetro no depende de la unidad de medida. Conforme aumenta la precisión del instrumento de medida (la unidad de medida es menor) nos acercamos más al valor exacto del perímetro.
Esta fue la revelación que se descubrió hace unas cuantas décadas y uno de los orígenes de una nueva Geometría: la Geometría Fractal. Pero eso no es todo, hay algo más que caracteriza a este tipo de líneas o de objetos: diferenciándole de las figuras geométricas que aprendemos en los institutos: la autosemejanza a distintas escalas. Esto quiere decir que si aumenta la escala a la que vemos un objeto, seguimos viendo una estructura semejante: las partes se parecen al todo. En la imagen inferior se muestra imágenes obtenidas con el Google de las Rías gallegas a distintas alturas sobre el suelo:

Rías gallegas a una altura de 50 Km, 10 Km y 2 Km de altura

Las costas, como las fronteras, están formadas por distintos cabos y golfos, los cuales a su vez están compuestos de entrantes y salientes y estos, a su vez, de ensenadas y riscos. Esto se puede observa a distintas escalas, desde 50 Km de altura, hasta en la escala a la que observa una hormiga.
Estas características: la nueva forma de medir el contorno y la autosemejanza no son sólo propias de las fronteras, sino que aparecen en muchos objetos en la naturaleza: nubes, hojas de un helecho, estructura de los árboles, romanescu, brócoli...

¿Imaginas medir el contorno de una nube? ¿Y el de la hoja de un helecho?
Lo que me hace recordar esa frase de Joseph Fourier, científico y matemático del siglo XIX que dijo que "El estudio profundo de la naturaleza es la fuente más fértil de descubrimientos matemáticos".
De todas formas, los fractales exactos son puramente matemáticos. En ellos, por mucho que aumentemos la escala nos volvemos a encontrar exactamente la misma estructura... Las partes se repiten hasta el infinito. Algo que no ocurre en la naturaleza. Y lo que es también chocante: encerrando un área finita, el perímetro tiende a ser infinito. Para saber más y ver fractales exactos, este enlace está bien: http://www.arrakis.es/~sysifus/

En este otro enlace, una actividad para hacer en secundaria, relacionada con la medida de costas: http://platea.pntic.mec.es/mzapata/tutor_ma/fractal/activ1_2.htm
Bibliografía:

• "Una nueva manera de ver el mundo. La geometría fractal". María Isabel Binimelis. Ediciones RBA
• "Caos fractales y cosas raras". Eliezer Braun. Fondo Cultura Económica.
• "Una introducción al mundo de los fracales". Parque de las Ciencias de Granada.
  

  • http://platea.pntic.mec.es/mzapata/tutor_ma/fractal/activ.htm

Imágenes:

• http://www.gran-angular.net/fractales-y-series-de-fibonacci-en-la-naturaleza/2008/09/11/
• http://www.asinah.net/portugalmap-es.html
• http://www.e-mapas.com/
• http://www.fotolog.com/re6is/27523329